Hacsak nem foglalkozik matematikával vagy programozással, az „algoritmus” szó görög lehet számodra, de ez az egyik építőköve mindannak, amelyet a cikk elolvasásához használsz. Itt van egy gyors magyarázat arról, hogy mik és hogyan működnek.
Jogi nyilatkozat: Nem vagyok matematika vagy informatika tanár, így az általam használt kifejezések közül nem mindegyik szakszerű. Ennek az az oka, hogy megpróbálok mindent egyszerű angolul elmagyarázni, mert az emberek nem nagyon érzik magukat a matematikában. Ennek ellenére van némi matematika, és ez elkerülhetetlen. Matek geekek, bátran javítsd ki vagy fejtsd ki jobban a megjegyzéseket, de kérlek, légy egyszerű a számunkra matematikailag elhatárolatlanok számára.
Kép készítette Ian Ruotsala
Mi az algoritmus?
Az „algoritmus” szónak az „algebra” -hoz hasonló etimológiája van, azzal a különbséggel, hogy ez magára az arab matematikusra, al-Khwarizmi-re vonatkozik (csak érdekes apróság). A köztünk lévő nem programozók számára egy algoritmus olyan utasításkészlet, amely bemenetet (A) és kimenetet (B) biztosít, amely valamilyen módon megváltoztatja az érintett adatokat. Az algoritmusok sokféle alkalmazással rendelkeznek. A matematikában segíthetnek a függvények kiszámításában az adatkészlet pontjaiból, sokkal fejlettebb dolgok között. Eltekintve attól, hogy magában a programozásban használják őket, fontos szerepet játszanak például a fájltömörítésben és az adatok titkosításában.
Alapvető utasításkészlet
Tegyük fel, hogy a barátod egy élelmiszerboltban találkozik veled, és te irányítod magad felé. Olyanokat mondasz, hogy „jöjj be a jobb oldali ajtókon”, „haladj át a hal részén a bal oldalon”, és „ha meglátod a tejüzemet, elhaladtál mellettem”. Az algoritmusok így működnek. Folyamatábra segítségével szemléltethetjük az utasításokat olyan kritériumok alapján, amelyeket időben ismerünk, vagy a folyamat során megtudunk.
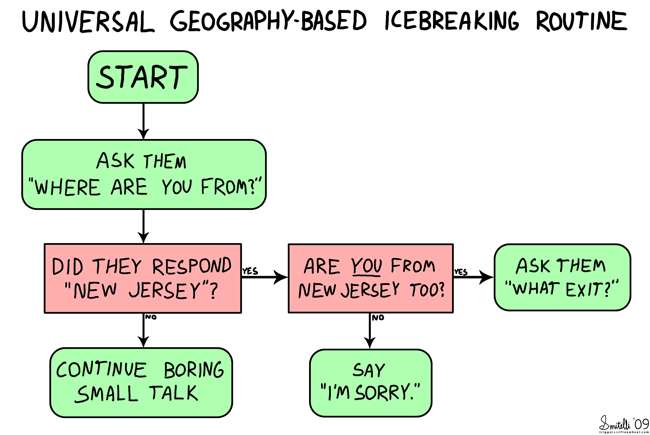
(kép címe: Jégtörő rutin ”EDIT: jóvoltából Indító és szabadonfutó )
A START-tól kezdve lefelé haladna az ösvényen, és attól függően, hogy mi történik, kövesse a „folyamatot” a végeredményig. A folyamatábra olyan vizuális eszköz, amely érthetőbben reprezentálhatja a számítógépek által használt utasítások halmazát. Hasonlóképpen, az algoritmusok ugyanezt segítik a több matematikai alapú modellnél.
Grafikonok
Használjuk egy grafikon segítségével az útbaigazítás különféle módjait.
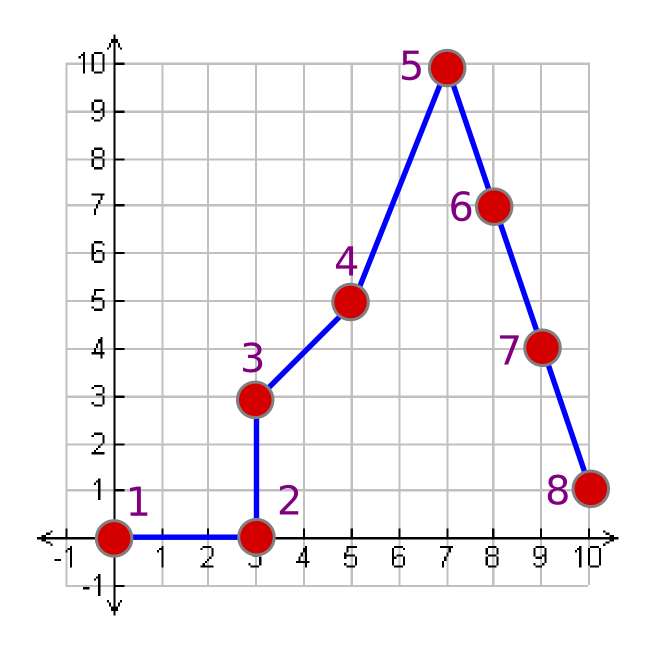
Kifejezhetjük ezt a gráfot az összes pontja közötti kapcsolatként. A kép reprodukálása érdekében utasításokat adhatunk másoknak.
1. módszer
Ezt pontsorozatként ábrázolhatjuk, és az információk a = {(x1, y1), (x2, y2), …, (xn, yn)} gráf szokásos formáját követnék.
grafikon = {(0,0), (3,0), (3,3), (5,5), (7,10), (8,7), (9,4), (10,1)}
Nagyon egyszerű az egyes pontok egymás utáni ábrázolása és összekapcsolása az előző ponttal. Képzeljen el egy grafikont, amelynek ezer pontja vagy több szegmense minden irányba halad. Ebben a listában sok adat lenne, igaz? És akkor fájdalmat okozhat, ha mindegyiket egyesével kell összekötni.
2. módszer
Egy másik dolog, amit tehetünk, megadunk egy kiindulási pontot, a közte és a következő pont közötti vonal meredekségét, és a = {(starting point}, [m1, x1, h1],…, [mn, xn, hn]} grafikon szokásos formájával jelezzük, hogy hol várható a következő pont. Itt az „m” változó az egyenes meredekségét jelöli, az „x” a számlálás irányát jelenti (akár x, akár y), a „h” pedig megmondja, hányat számoljon az említett irányban. Emlékezhet arra is, hogy minden mozdulat után megrajzol egy pontot.
grafikon = {(0,0), [0,x,3], [0,y,3], [1,x,2], [2.5,x,2], [-3,x,1], [-3,x,1], [-3,x,1]}
Végül ugyanaz a grafikon jelenik meg. Láthatja, hogy ebben a kifejezésben az utolsó három kifejezés megegyezik, ezért képesek vagyunk levágni ezt azzal, hogy valamilyen módon csak azt mondjuk, hogy „ismételje meg ezt háromszor”. Tegyük fel, hogy bármikor megjelenik az „R” változó, ez azt jelenti, hogy megismételjük az utolsó dolgot. Meg tudjuk csinálni:
grafikon = {(0,0), [0,x,3], [0,y,3], [1,x,2], [2.5,x,2], [-3,x,1], [R=2]}
Mi van, ha az egyes pontok nem igazán számítanak, és csak maga a grafikon számít? Összevonhatjuk az utóbbi három szakaszt így:
grafikon = {(0,0), [0,x,3], [0,y,3], [1,x,2], [2.5,x,2], [-3,x,3]}
Kicsit lerövidíti a dolgokat abból a helyből, ahol korábban voltak.
3. módszer
Próbáljuk meg ezt más módon megtenni.
y = 0, 0≤x≤3
x = 0, 0≤y≤3
y = x, 3≤x≤5
y = 2,5x-7,5, 5≤x≤7
y = -3x + 29, 7≤x≤8
y = -3x + 29, 8≤x≤9
y = -3x + 29,9≤x≤10
Itt tiszta algebrai kifejezésekkel rendelkezünk. Még egyszer: ha maguk a pontok nem számítanak, és csak a grafikon számít, akkor az utolsó három elemet konszolidálhatjuk.
y = 0, 0≤x≤3
x = 0, 0≤y≤3
y = x, 3≤x≤5
y = 2,5x-7,5, 5≤x≤7
y = -3x + 29, 7≤x≤10
Most melyik módszert választja, a képességeitől függ. Talán remekül értesz a matekhoz és a grafikonokhoz, ezért az utolsó lehetőséget választod. Talán jól tud navigálni, ezért a második lehetőséget választja. A számítógépek területén azonban sokféle feladatot végez, és a számítógép képességei nem igazán változnak. Ezért az algoritmusokat optimalizálják az általuk elvégzett feladatokhoz.
Egy másik fontos szempont, hogy mindegyik módszer egy kulcsra támaszkodik. Minden utasításkészlet haszontalan, hacsak nem tudsz mit kezdeni velük. Ha nem tudod, hogy minden pontot meg kell ábrázolnod és összekapcsolnod a pontokat, az első pontkészlet nem jelent semmit. Hacsak nem tudja, hogy az egyes változók mit jelentenek a második módszerben, nem fogja tudni, hogyan kell alkalmazni őket, hasonlóan a titkosítás kulcsához. Ez a kulcs az algoritmusok használatának is szerves része, és gyakran ez a kulcs megtalálható a közösségben vagy egy „szabvány” révén.
Fájltömörítés
Amikor letölti a .zip fájlokat, kibontja a tartalmát, hogy a benne lévő tartalmat felhasználhassa. Manapság a legtöbb operációs rendszer úgy merülhet el .zip fájlokban, mintha normál mappák lennének, és mindent megtesznek a háttérben. Több mint egy évtizeddel ezelõtt Windows 95-ös gépemen mindent manuálisan kellett kibontanom, mielõtt többet láttam, mint a fájlneveket. Ez azért van, mert amit a lemezen .zip fájlként tároltak, az nem volt használható formában. Gondoljon egy kihúzható kanapéra. Ha ágyként akarja használni, el kell távolítania a párnákat és szét kell hajtania, ami több helyet foglal. Ha nincs rá szüksége, vagy ha szállítani akarja, akkor visszahajthatja.
A tömörítési algoritmusokat kifejezetten azoknak a fájltípusoknak megfelelően állítják be és optimalizálják, amelyekre megcélozzák. Az audio formátumok például mindegyik más módon tárolja az adatokat, amelyek az audio kodek által dekódolva az eredeti hullámformához hasonló hangfájlt adnak. Ha többet szeretne tudni ezekről a különbségekről, olvassa el előző cikkünket, Mi a különbség az összes audio formátum között? A veszteségmentes audioformátumok és a .zip fájlok egy közös vonást mutatnak: mindkettő a dekompressziós folyamat után az eredeti adatokat pontos formájában adja. A vesztes audiokodekek más eszközökkel spórolják meg a lemezterületet, például olyan frekvenciákat nyírnak, amelyeket az emberi fülek nem hallanak, és szakaszokban kisimítják a hullámformát, hogy megszabaduljanak néhány részlettől. Végül, bár lehet, hogy nem igazán halljuk a különbséget egy MP3 és egy CD-sáv között, az előbbiben mindenképpen hiányos az információ.
Adat titkosítás
Algoritmusokat is használnak az adatok vagy a kommunikációs vonalak biztosításához. Az adatok tárolása helyett, hogy kevesebb lemezterületet használjon fel, más programok által nem észlelhető módon tárolják. Ha valaki ellopja a merevlemezt és elkezdi vizsgálni, akkor is felveheti az adatokat, még akkor is, ha fájlokat töröl, mert maga az adat még mindig ott van, annak ellenére, hogy az átirányítási hely eltűnt. Az adatok titkosításakor a tárolt adatok nem úgy néznek ki, mint amilyenek. Általában véletlenszerűen néz ki, mintha a széttagoltság idővel felépült volna. Tárolhat adatokat is, és más fájltípusként is megjelenítheti azokat. A képfájlok és a zenefájlok erre jók, mivel elég nagyok lehetnek például anélkül, hogy gyanút keltenének. Mindezt matematikai algoritmusok segítségével hajtják végre, amelyek valamilyen bemenetet igényelnek, és átalakítanak egy másik, nagyon specifikus kimenetre. További információ a titkosítás működéséről: A HTG elmagyarázza: Mi a titkosítás és hogyan működik?
Az algoritmusok matematikai eszközök, amelyek sokféle felhasználási lehetőséget kínálnak a számítástechnikában. Azon dolgoznak, hogy a kiindulási pont és a végpont között következetes módon biztosítsák az utat, és útmutatást adnak annak követésére. Tud többet, mint amit kiemeltünk? Ossza meg magyarázatait a megjegyzésekben!
