Med mindre du er interessert i matematikk eller programmering, kan ordet "algoritme" være gresk for deg, men det er en av byggesteinene i alt du bruker for å lese denne artikkelen. Her er en rask forklaring på hva de er, og hvordan de fungerer.
Ansvarsfraskrivelse: Jeg er ikke en matte- eller informatikklærer, så ikke alle begrepene jeg bruker er tekniske. Det er fordi jeg prøver å forklare alt på vanlig engelsk, for folk er ikke helt komfortable med matematikk. Når det er sagt, er det noe matte involvert, og det er uunngåelig. Math geeks, kan du rette eller bedre forklare i kommentarene, men vær så snill, hold det enkelt for de matematisk tilbøyelige blant oss.
Bilde av Ian Ruotsala
Hva er en algoritme?
Ordet ‘algoritme’ har en etymologi som ligner på ‘algebra,’ bortsett fra at dette refererer til den arabiske matematikeren selv, al-Khwarizmi (bare en interessant godbit). En algoritme, for ikke-programmerere blant oss, er et sett med instruksjoner som tar en inngang, A, og gir en utgang, B, som endrer dataene som er involvert på en eller annen måte. Algoritmer har et bredt spekter av applikasjoner. I matematikk kan de hjelpe til med å beregne funksjoner fra poeng i et datasett, blant mye mer avanserte ting. Bortsett fra deres bruk i selve programmeringen, spiller de store roller i ting som filkomprimering og datakryptering.
Et grunnleggende sett med instruksjoner
La oss si at vennen din møter deg i en matbutikk, og du veileder ham mot deg. Du sier ting som "komme inn gjennom dørene til høyre", "passere fiskeseksjonen til venstre" og "hvis du ser meieriet, gikk du forbi meg." Algoritmer fungerer slik. Vi kan bruke et flytskjema for å illustrere instruksjoner basert på kriterier vi kjenner til på forhånd eller finner ut underveis i prosessen.
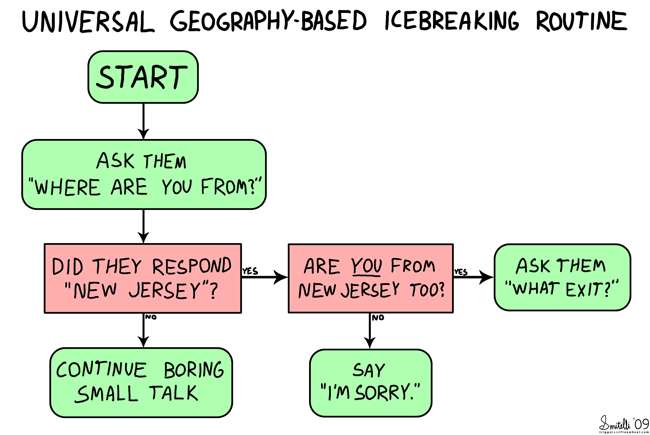
(bilde med tittelen “ Isbrytende rutine ”EDIT: høflighet av Utløser og friløp )
Fra START vil du gå nedover stien, og avhengig av hva som skjer følger du "strømmen" til et sluttresultat. Flytskjemaer er visuelle verktøy som mer forståelig kan representere et sett med instruksjoner som brukes av datamaskiner. Tilsvarende hjelper algoritmer med å gjøre det samme med mer mattebaserte modeller.
Grafer
La oss bruke en graf for å illustrere de forskjellige måtene vi kan gi veibeskrivelse på.
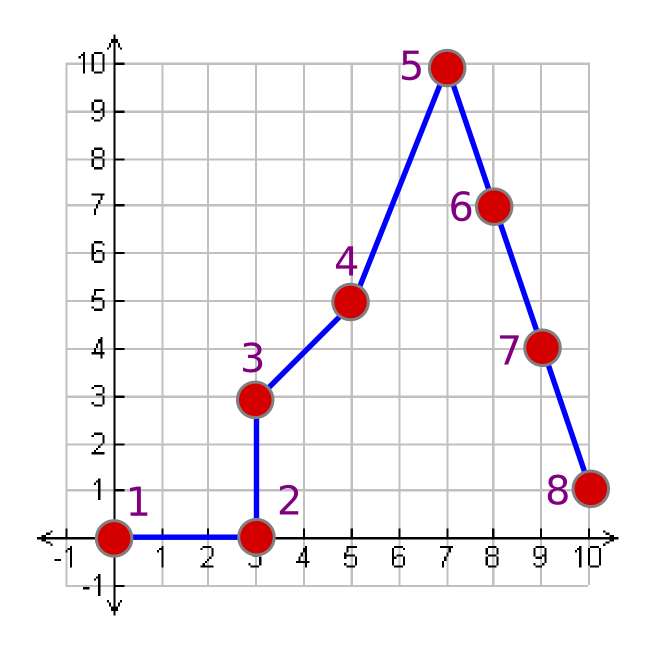
Vi kan uttrykke denne grafen som en sammenheng mellom alle dens punkter. For å gjengi dette bildet, kan vi gi et sett med instruksjoner til noen andre.
Metode 1
Vi kan representere dette som en serie punkter, og informasjonen vil følge standardformen for graf = {(x1, y1), (x2, y2), …, (xn, yn)}.
graf = {(0,0), (3,0), (3,3), (5,5), (7,10), (8,7), (9,4), (10,1)}
Det er ganske enkelt å plotte hvert punkt, det ene etter det andre, og koble dem til det forrige punktet. Tenk deg imidlertid en graf med tusen poeng eller flere segmenter som alle går hver vei. Den listen ville ha mye data, ikke sant? Og å måtte koble hver enkelt, en om gangen, kan være vondt.
Metode 2
En annen ting vi kan gjøre er å gi et startpunkt, stigningen på linjen mellom det og neste punkt, og indikere hvor du kan forvente det neste punktet ved hjelp av standardformen for graf = {(starting point}, [m1, x1, h1],…, [mn, xn, hn]}. Her representerer variabelen ‘m’ skråningen på linjen, ‘x’ representerer retningen du skal telle i (enten x eller y), og ‘h’ forteller deg hvor mange du skal telle i nevnte retning. Du kan også huske å plotte et poeng etter hver bevegelse.
graf = {(0,0), [0,x,3], [0,y,3], [1,x,2], [2.5,x,2], [-3,x,1], [-3,x,1], [-3,x,1]}
Du vil ende opp med den samme grafen. Du kan se at de tre siste begrepene i dette uttrykket er de samme, så vi kan kanskje trimme det ned ved bare å si "gjenta det tre ganger" på en eller annen måte. La oss si at når som helst du ser variabelen 'R' vises, betyr det å gjenta det siste. Vi kan gjøre dette:
graf = {(0,0), [0,x,3], [0,y,3], [1,x,2], [2.5,x,2], [-3,x,1], [R=2]}
Hva om de enkelte punktene ikke egentlig betyr noe, og bare selve grafen gjør det? Vi kan konsolidere de tre siste seksjonene slik:
graf = {(0,0), [0,x,3], [0,y,3], [1,x,2], [2.5,x,2], [-3,x,3]}
Det forkorter ting litt fra der de var før.
Metode 3
La oss prøve å gjøre dette på en annen måte.
y = 0, 0≤x≤3
x = 0, 0≤y≤3
y = x, 3≤x≤5
y = 2,5x-7,5, 5≤x≤7
y = -3x + 29, 7≤x≤8
y = -3x + 29, 8≤x≤9
y = -3x + 29,9≤x≤10
Her har vi det i rene algebraiske termer. Nok en gang, hvis selve punktene ikke betyr noe, og bare grafen gjør det, kan vi konsolidere de tre siste elementene.
y = 0, 0≤x≤3
x = 0, 0≤y≤3
y = x, 3≤x≤5
y = 2,5x-7,5, 5≤x≤7
y = -3x + 29, 7≤x≤10
Nå, hvilken metode du velger, avhenger av dine evner. Kanskje du er flott med matematikk og grafer, så du velger det siste alternativet. Kanskje du er flink til å navigere, så du velger det andre alternativet. I datamaskinene utfører du imidlertid mange forskjellige typer oppgaver, og datamaskinens evne endres ikke. Derfor er algoritmer optimalisert for oppgavene de fullfører.
Et annet viktig poeng å merke seg er at hver metode er avhengig av en nøkkel. Hvert sett med instruksjoner er ubrukelig med mindre du vet hva du skal gjøre med dem. Hvis du ikke vet at du skal plotte hvert punkt og koble sammen punktene, betyr det første settet med poeng ingenting. Med mindre du vet hva hver variabel betyr i den andre metoden, vet du ikke hvordan du bruker dem, omtrent som nøkkelen til en kryptering. Den nøkkelen er også en integrert del av bruk av algoritmer, og ofte blir den nøkkelen funnet i samfunnet eller via en "standard".
Filkomprimering
Når du laster ned en .zip-fil, trekker du ut innholdet slik at du kan bruke det som er inne i den. I dag kan de fleste operativsystemer dykke ned i .zip-filer som om de var normale mapper, og gjorde alt i bakgrunnen. På Windows 95-maskinen min for over et tiår siden måtte jeg trekke ut alt manuelt før jeg kunne se noe mer enn filnavnene inne. Det er fordi det som ble lagret på disken som en .zip-fil, ikke var i brukbar form. Tenk på en uttrekkbar sofa. Når du vil bruke den som en seng, må du fjerne putene og brette den ut, noe som tar mer plass. Når du ikke trenger det, eller hvis du vil transportere det, kan du brette det opp igjen.
Komprimeringsalgoritmer justeres og optimaliseres spesifikt for filtypene de er målrettet mot. Lydformater bruker for eksempel hver sin måte å lagre data på som, når de dekodes av lydkodeken, gir en lydfil som ligner på den opprinnelige bølgeformen. For mer informasjon om forskjellen, sjekk ut forrige artikkel, Hva er forskjellen mellom alle disse lydformatene? Tapte lydformater og .zip-filer har en ting til felles: de gir begge originaldataene i sin eksakte form etter dekompresjonsprosessen. Tapte lydkodeker bruker andre midler for å spare diskplass, for eksempel beskjæring av frekvenser som ikke kan høres av menneskelige ører, og utjevning av bølgeformen i seksjoner for å kvitte seg med noen detaljer. Til slutt, selv om vi kanskje ikke virkelig kan høre forskjellen mellom en MP3 og et CD-spor, er det definitivt et underskudd på informasjon i det tidligere.
Datakryptering
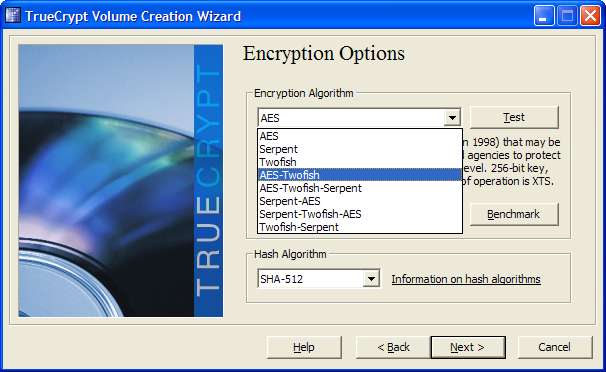
Algoritmer brukes også ved sikring av data eller kommunikasjonslinjer. I stedet for å lagre data slik at de bruker mindre diskplass, lagres de på en måte som ikke kan oppdages av andre programmer. Hvis noen stjeler harddisken din og begynner å skanne den, kan de hente data selv når du sletter filer fordi selve dataene fremdeles er der, selv om videresendingsplasseringen til den er borte. Når data er kryptert, ser det som er lagret ikke ut som det er. Det ser vanligvis tilfeldig ut, som om fragmentering hadde bygget seg opp over tid. Du kan også lagre data og få dem til å fremstå som en annen type fil. Bildefiler og musikkfiler er bra for dette, da de for eksempel kan være ganske store uten å få mistanke. Alt dette gjøres ved å bruke matematiske algoritmer, som tar en slags input og konverterer den til en annen, veldig spesifikk type output. For mer informasjon om hvordan kryptering fungerer, sjekk ut HTG forklarer: Hva er kryptering og hvordan fungerer det?
Algoritmer er matematiske verktøy som gir en rekke bruksområder innen informatikk. De jobber for å gi en sti mellom et startpunkt og et sluttpunkt på en konsekvent måte, og gir instruksjonene for å følge det. Vet du mer enn det vi fremhevet? Del forklaringene dine i kommentarene!