אלא אם כן אתה עוסק במתמטיקה או בתכנות, המילה "אלגוריתם" עשויה להיות יוונית עבורך, אך זוהי אחת מאבני הבניין של כל מה שאתה משתמש כדי לקרוא מאמר זה. הנה הסבר מהיר על מה הם ואיך הם עובדים.
הצהרת אחריות: אני לא מורה למתמטיקה או מדעי המחשב, ולכן לא כל המונחים בהם אני משתמש הם טכניים. הסיבה לכך היא שאני מנסה להסביר הכל באנגלית רגילה עבור אנשים שלא ממש מרגישים בנוח עם מתמטיקה. עם זאת, יש איזושהי מתמטיקה מעורבת, וזה בלתי נמנע. גיקים במתמטיקה, אתם מוזמנים לתקן או להסביר טוב יותר את ההערות, אך אנא, שמרו על כך פשוט לחסרי המתמטיקה שבינינו.
תמונה מאת איאן רוטסלה
מהי אלגוריתם?
למילה 'אלגוריתם' יש אטימולוגיה הדומה ל'אלגברה ', אלא שהכוונה היא למתמטיקאי הערבי עצמו, אל-ח'ווריזמי (סתם עניין מעניין). אלגוריתם, עבור הלא מתכנתים שבינינו, הוא מערכת הוראות שלוקחות קלט, A, ומספקות פלט, B, שמשנה את הנתונים המעורבים בדרך כלשהי. לאלגוריתמים יש מגוון רחב של יישומים. במתמטיקה הם יכולים לעזור בחישוב פונקציות מנקודות בערכת נתונים, בין דברים מתקדמים הרבה יותר. מלבד השימוש שלהם בתכנות עצמו, הם ממלאים תפקידים מרכזיים בדברים כמו דחיסת קבצים והצפנת נתונים.
סט הוראות בסיסי
בוא נגיד שחבר שלך פוגש אותך במכולת ואתה מנחה אותו לעברך. אתה אומר דברים כמו "להיכנס דרך הדלתות הימניות", "לעבור את קטע הדגים מצד שמאל" ו"אם אתה רואה את המחלבה, עברת לידיי. " אלגוריתמים עובדים ככה. אנו יכולים להשתמש בתרשים זרימה כדי להמחיש הוראות המבוססות על קריטריונים שאנו מכירים מבעוד מועד או לברר במהלך התהליך.
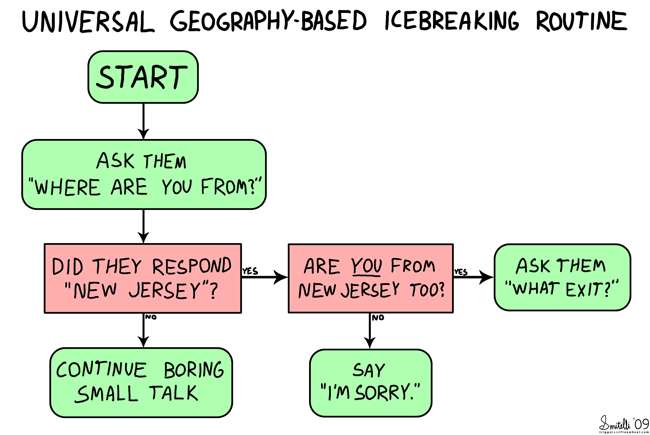
(תמונה שכותרתה “ שגרת שבירת קרח עריכה: באדיבות טריגר וגלגל חופשי )
מ- START, היית הולך בשביל, ובהתאם למה שקורה אתה עוקב אחר "הזרימה" לתוצאה סופית. תרשימי זרימה הם כלים ויזואליים שיכולים לייצג באופן מובן יותר מערך הוראות המשמש מחשבים. באופן דומה, אלגוריתמים עוזרים לעשות את אותו הדבר עם מודלים מבוססי מתמטיקה יותר.
גרפים
בואו נשתמש בגרף כדי להמחיש את הדרכים השונות בהן אנו יכולים לתת הוראות.
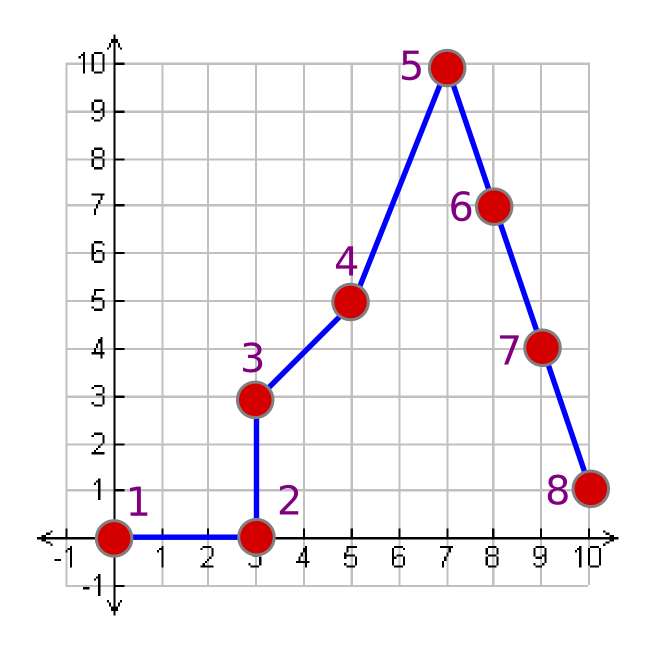
אנו יכולים לבטא גרף זה כחיבור בין כל הנקודות שלו. על מנת לשחזר תמונה זו, אנו יכולים לתת סט הוראות למישהו אחר.
שיטה 1
אנו יכולים לייצג זאת כסדרת נקודות, והמידע יתבצע בצורה הסטנדרטית של גרף = {(x1, y1), (x2, y2), …, (xn, yn)}.
גרף = {(0,0), (3,0), (3,3), (5,5), (7,10), (8,7), (9,4), (10,1)}
די קל לתכנן כל נקודה, אחת אחרי השנייה, ולחבר אותן לנקודה הקודמת. עם זאת, דמיין גרף עם אלף נקודות או קטעים מרובים שהולכים לכל כיוון. ברשימה זו יהיו נתונים רבים, נכון? ואז הצורך לחבר כל אחד, אחד בכל פעם, יכול להיות כאב.
שיטה 2
דבר נוסף שאנו יכולים לעשות הוא לתת נקודת התחלה, את שיפוע הקו בינה לנקודה הבאה, ולציין היכן ניתן לצפות לנקודה הבאה באמצעות הצורה הסטנדרטית של גרף = {(starting point}, [m1, x1, h1], ..., [mn, xn, hn]}. כאן, המשתנה 'm' מייצג את שיפוע הקו, 'x' מייצג את הכיוון לספור בו (בין אם x או y), ו- 'h' אומר לך כמה לספור בכיוון האמור. אתה יכול גם לזכור לשרטט נקודה אחרי כל תנועה.
גרף = {(0,0), [0,x,3], [0,y,3], [1,x,2], [2.5,x,2], [-3,x,1], [-3,x,1], [-3,x,1]}
בסוף תקבל אותו גרף. אתה יכול לראות ששלושת המונחים האחרונים בביטוי זה זהים, כך שנוכל לקצץ זאת רק על ידי אמירה "חזור על זה שלוש פעמים" בדרך כלשהי. בואו נגיד שבכל פעם שאתם רואים את המשתנה 'R' מופיע, זה אומר לחזור על הדבר האחרון. אנחנו יכולים לעשות את זה:
גרף = {(0,0), [0,x,3], [0,y,3], [1,x,2], [2.5,x,2], [-3,x,1], [R=2]}
מה אם הנקודות הבודדות לא באמת חשובות, ורק הגרף עצמו כן? אנו יכולים לאחד את שלושת הסעיפים האחרונים כך:
גרף = {(0,0), [0,x,3], [0,y,3], [1,x,2], [2.5,x,2], [-3,x,3]}
זה מקצר את העניינים מעט מהמקום שהיה בו קודם.
שיטה 3
בואו ננסה לעשות זאת בדרך אחרת.
y = 0, 0≤x≤3
x = 0, 0≤y≤3
y = x, 3≤x≤5
y = 2.5x-7.5, 5≤x≤7
y = -3x + 29, 7≤x≤8
y = -3x + 29, 8≤x≤9
y = -3x + 29.9≤x≤10
הנה לנו במונחים אלגבריים טהורים. שוב, אם הנקודות עצמן לא חשובות ורק הגרף כן, נוכל לאחד את שלושת הפריטים האחרונים.
y = 0, 0≤x≤3
x = 0, 0≤y≤3
y = x, 3≤x≤5
y = 2.5x-7.5, 5≤x≤7
y = -3x + 29, 7≤x≤10
עכשיו, איזו שיטה תבחר תלויה ביכולות שלך. אולי אתה מצוין עם מתמטיקה וגרפים, אז אתה בוחר באפשרות האחרונה. אולי אתה טוב בניווט, אז אתה בוחר באפשרות השנייה. בתחום המחשבים, לעומת זאת, אתה מבצע סוגים רבים ושונים של משימות ויכולת המחשב לא באמת משתנה. לכן, האלגוריתמים מותאמים למשימות שהם מסיימים.
נקודה חשובה נוספת שיש לציין היא שכל שיטה מסתמכת על מפתח. כל סט הוראות אינן חסרות תועלת אלא אם כן אתה יודע מה לעשות איתן. אם אתה לא יודע שאתה אמור לשרטט כל נקודה ולחבר את הנקודות, סט הנקודות הראשון לא אומר כלום. אלא אם כן אתה יודע מה המשמעות של כל משתנה בשיטה השנייה, לא תדע ליישם אותם, ממש כמו המפתח לצופן. מפתח זה הוא גם חלק בלתי נפרד משימוש באלגוריתמים, ולעתים קרובות מפתח זה נמצא בקהילה או באמצעות "תקן".
דחיסת קבצים
כשאתה מוריד קובץ zip, אתה מחלץ את התוכן כדי שתוכל להשתמש בכל מה שיש בתוכו. כיום, רוב מערכות ההפעלה יכולות לצלול לקבצי zip כאילו היו תיקיות רגילות, ולעשות הכל ברקע. במכשיר Windows 95 שלי לפני למעלה מעשור נאלצתי לחלץ הכל ידנית לפני שהספקתי לראות יותר משמות הקבצים שבפנים. הסיבה לכך היא שמה שנשמר בדיסק כקובץ ZIP לא היה בצורה שמישה. תחשוב על ספה נשלפת. כשרוצים להשתמש בו כמיטה, עליכם להסיר את הכריות ולפרוש אותן, מה שתופס יותר מקום. כאשר אינך זקוק לו, או אם ברצונך להעבירו, תוכל לקפל אותו בחזרה.
אלגוריתמי דחיסה מותאמים ומותאמים במיוחד לסוגי הקבצים אליהם הם מכוונים. פורמטי שמע, למשל, כל אחד מהם משתמש בדרך אחרת לאחסון נתונים שכאשר הם מפוענחים על ידי קוד האודיו, הם ייתן קובץ קול הדומה לצורת הגל המקורית. למידע נוסף על ההבדל, עיין במאמר הקודם שלנו, מה ההבדל בין כל אותם פורמטי שמע? לפורמטים שמע ללא אובדן ולקבצי zip יש דבר משותף: שניהם מניבים את הנתונים המקוריים בצורתם המדויקת לאחר תהליך הדחיסה. רכיבי codec שמע אובדנים משתמשים באמצעים אחרים כדי לחסוך מקום בדיסק, כמו זמירה של תדרים שאינם מסוגלים להישמע באוזניים אנושיות והחלקת צורת הגל בחלקים כדי להיפטר מפרטים מסוימים. בסופו של דבר, למרות שאולי לא נצליח לשמוע באמת את ההבדל בין רצועת MP3 לתקליטור, בהחלט יש גירעון של מידע בראשון.
הצפנת מידע
אלגוריתמים משמשים גם בעת אבטחת נתונים או קווי תקשורת. במקום לאחסן נתונים כך שישתמשו בפחות שטח דיסק, הם נשמרים באופן שלא ניתן לזהות על ידי תוכניות אחרות. אם מישהו גונב את הכונן הקשיח שלך ומתחיל לסרוק אותו, הוא יכול לאסוף נתונים גם כאשר אתה מוחק קבצים מכיוון שהנתונים עצמם עדיין שם, למרות שמיקום ההעברה אליו נעלם. כאשר הנתונים מוצפנים, כל מה שנשמר לא נראה כמו מה שהם. זה בדרך כלל נראה אקראי, כאילו פיצול נבנה עם הזמן. ניתן גם לאחסן נתונים ולגרום להם להופיע כסוג אחר של קובץ. קבצי תמונה וקבצי מוזיקה טובים לכך, מכיוון שהם יכולים להיות גדולים למדי מבלי לחשוד, למשל. כל זה נעשה על ידי שימוש באלגוריתמים מתמטיים, שלוקחים קלט כלשהו והופכים אותו לסוג אחר של פלט ספציפי. למידע נוסף על אופן פעולת ההצפנה, עיין ב HTG מסביר: מהי הצפנה ואיך זה עובד?
אלגוריתמים הם כלים מתמטיים המספקים מגוון שימושים במדעי המחשב. הם פועלים לספק נתיב בין נקודת התחלה לנקודת סיום באופן עקבי, ומספקים את ההוראות לעקוב אחריה. יודעים יותר ממה שהדגשנו? שתף את ההסברים שלך בתגובות!